6.046 incremental improvement

Algorithms › 6.046 algorithms design

Flow networks

Notions+

  • directed graph G(V, E)
  • two distinguished vertices source s, sink t
  • basic idea: flow comes out of s and makes it way to t with constraints on edges.
    • capacity is like the amount of traffic that can go through the road; flow goes through the edge.
    • local contraint: the flow can never exceed the capacity
    • flow: think flow as a rate. No commodity accumulation along the way. Flow can be cyclic
  • cut is a partition of nodes. A cut in G forms two disconnected components.

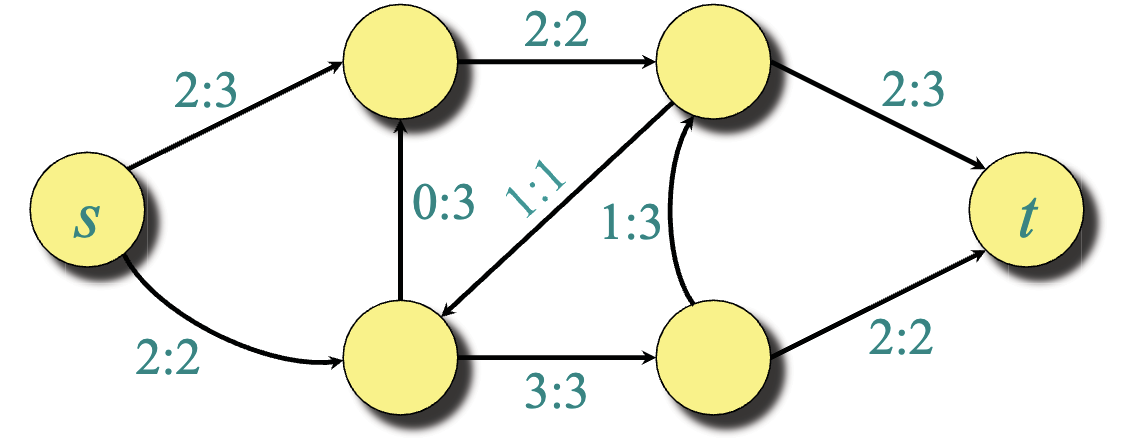
Example: each edge (u, v) in E, non-negative capacity c(u, v). If (u, v) not in E, then assume c(u, v) = 0

Maximum-flow problem: Given a flow network G, find a flow of maximum value on G.

Assumptions:

  1. no self-loop edges allowed
  2. If edge(u, v) in E exists, then (v, u) not in E. WLOG, introduce a new vertex u’ so that v -> u’ -> u

Relation of flow and cut: The capacity of any cut bounds the flow of cut/network. Min-cut will point to the max-flow.

Flow

Flow: A (net) flow on G is function f: V*V -> R satisfying the following constrains.

  • Capacity constraint: For all u,v V, f(u, v) <= c(u, v).

  • Flow conservation: For all u V - {s, t},

  • Skew symmetry: For all u,v V, f(u, v) = -f(v, u)

The value of a flow f,

Simple properties of flow:

1. f(X, X) = 0, f(X, Y) = - f(Y, X), if .

1. , what goes out the source is what goes in the sink.

Proof. , flow of the intermediate vertices goes out to all vertices by conservation law.

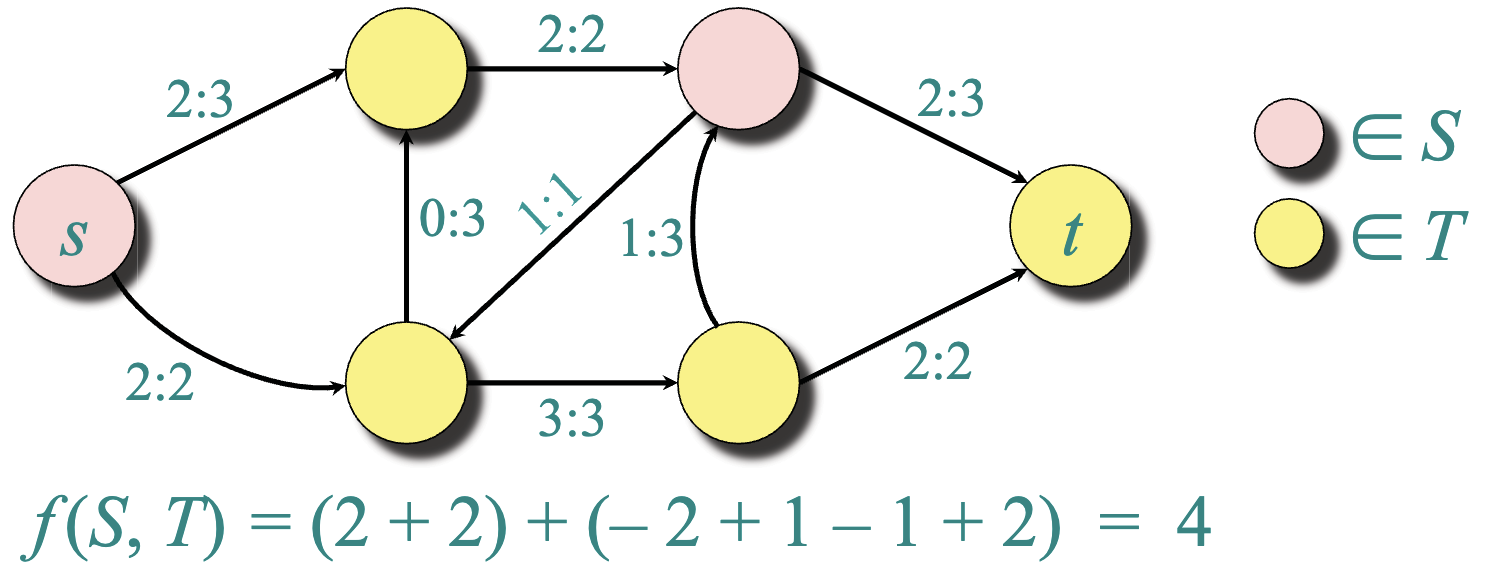
Cut

  1. the flow across the cut is as the sum of flows corresponding to each pair of vertices (crossing edges).
  2. capacity of cut c(S, T) = 3+2+3+1=9

Cut: A cut (S< T) of a flow network G = (V, E) is a partition of V such that s S and t T. If f is a low on G, then the flow across the cut is f(S, T)

2. The value of any flow is bounded by the capacity of any cut.

2. For any flow f and any cut (S, T), we have .

Proof of T2. =

Proof of L2.

  • Intuitively, source is on one side of the cut and sink on the other side.
  • : , by conservation law

Residual networks

  1. network points to where you can increase the flow for capacity left.
  2. Augmentation: Not only increase the flow but also shrink it. The shrinkage of flow is represented by an edge in the residual network.
  3. How augmentation changes flow: walking through the augmenting path, looking at each of the residual capacities and picking the Min value.
  4. Help to look for augmenting paths in Gf for Ford Fulkerson.

Residual network: , strictly positive residual capacities . Edges in admit more flow.

If (v, u) not in E, c(v, u) = 0, but f(v, u) = -f(u, v).

Augmenting paths:

  1. graph G => residual networks Gf => augmented paths

    • G:

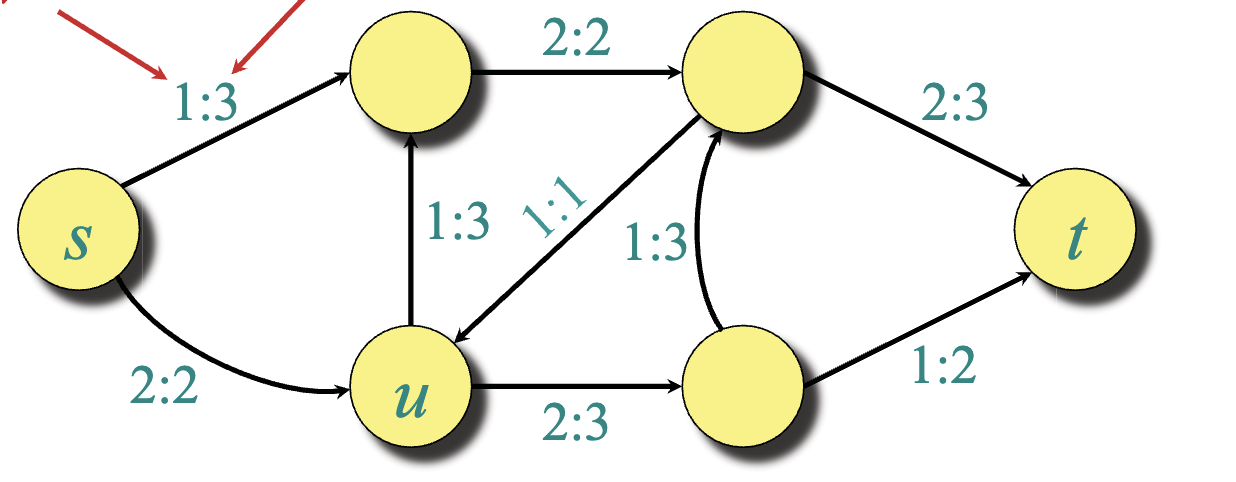
    • Gf:

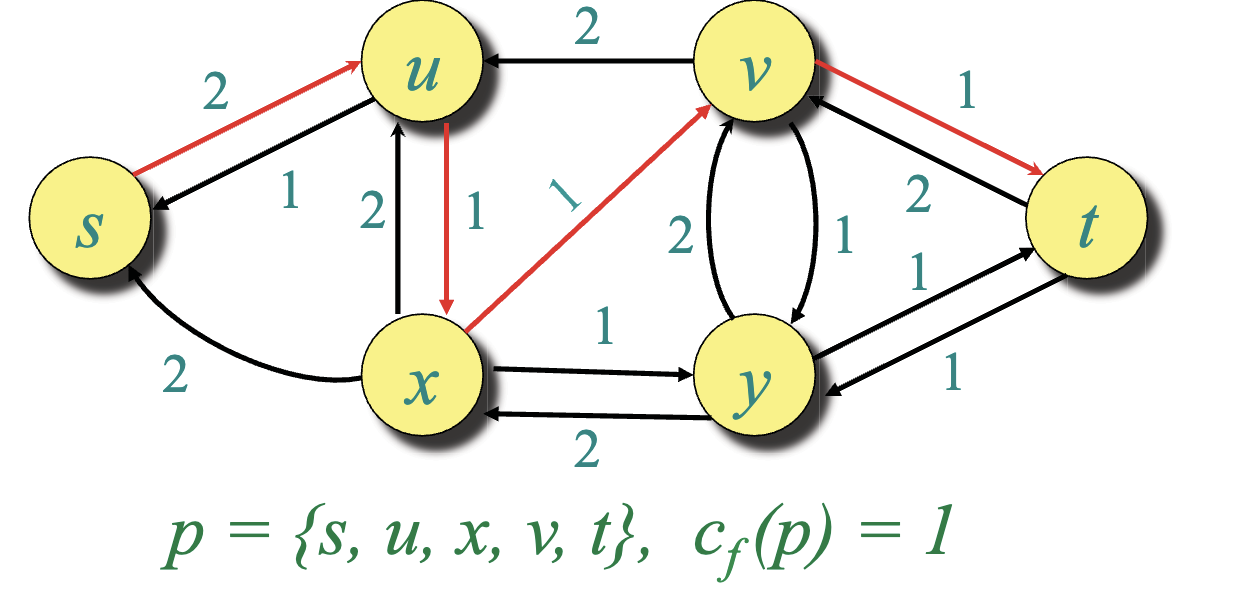
  2. If find a path from s to t in , then the flow is not maximum. If no path exists, the flow is maximum.

  3. Augmenting paths can increase flow and tell how to change edges (subtract or increase)

Any path from s to t in is an augmenting path in G with respect to f. The flow value can be increased along an augmenting path p by .

Max-flow, min-cut

Max-flow, min-cut theorem

Proof: 1=>2, 2=>3, 3=>1. Movement between Gf and G.

3. The following are equivalent:

  1. for some cut (S, T). => some cut is saturated
  2. f is a maximum flow.
  3. f admits no augmenting paths.

Proof.

  • 1=>2, for any cut (S, T)

  • 2=>3, by contradiction

  • 3=>1, suppose f admits no augmenting paths (cannot reach t from s)

    • Define S = {vV: there exists a path in Gf from s to v} (set of the reachable vertices from S) and let T = V - S (sS, tT=>(S, T) is a cut)

    • key observation: no path in Gf from u to v, otherwise v S.

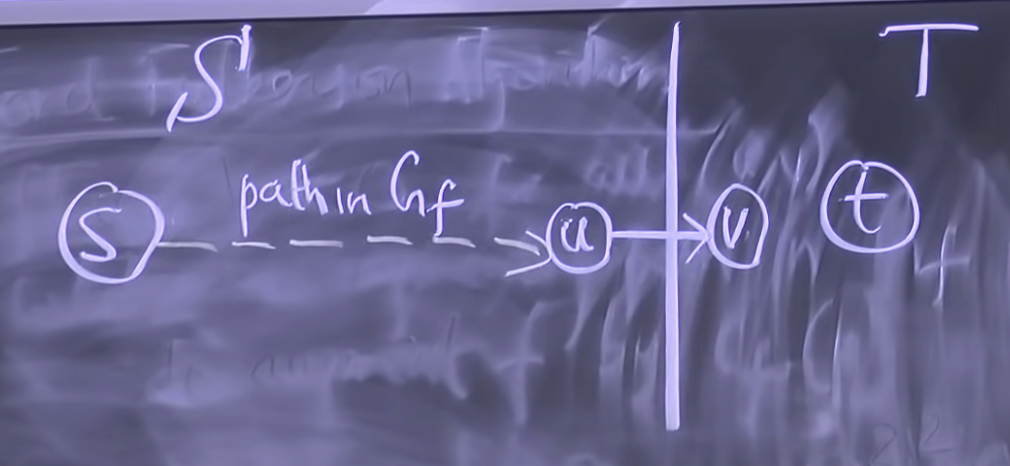
      • Picking an edge in G from u to v with a non-zero capacity (existence)

    • => , since if , then vS not vT as assumed.

    • => f(u, v) = c(u, v), every edge from S to T in G is saturated => summing over u, v … yields f(S, T) = c(S, T).

Ford-Fulkerson algorithm

  1. many subproblem routines: compute Gf given f, discover an augmenting path via dfs/bfs, …
  2. proof: prove T3: 3=>2
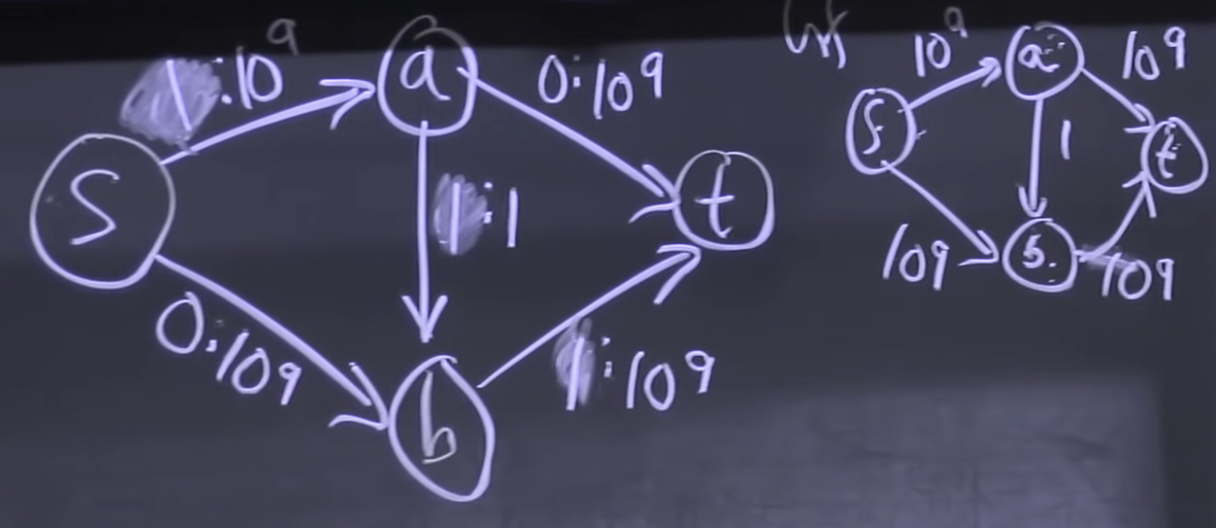
  3. What selected paths lead to failure:
    • only need 2 iterations in the example
    • It takes 2 billion iterations: s->a->b (G) => s->b->a (Gf) => G => Gf …

f[u, v] <- 0 for all u,v V. While an augmenting path p in Gf exists, do augment f by

Edmonds-Karp algorithm

  1. breadth-first () or depth-first can provide a polynomial-time bound on max flow
  2. runtime:
    • augmentations in worst case
    • overall complexity
  3. fastest max flow algorithms O(VE), Orlin 2015

breadth-first augmenting path: a shortest path in Gf from s to t where each edge has weight 1.

Baseball elimination ex

Rules: divisions: playoffs -> tied: elimination. Team i is eliminated if wi + ri < wj for some j. are the games that these teams play against each other. Table 1 only lists one division. ri includes games playing against other divisions.

Problem: Decide if you have a chance to make the playoffs or not. Want an algorithms to look at standings and decide if the team is alive or not.

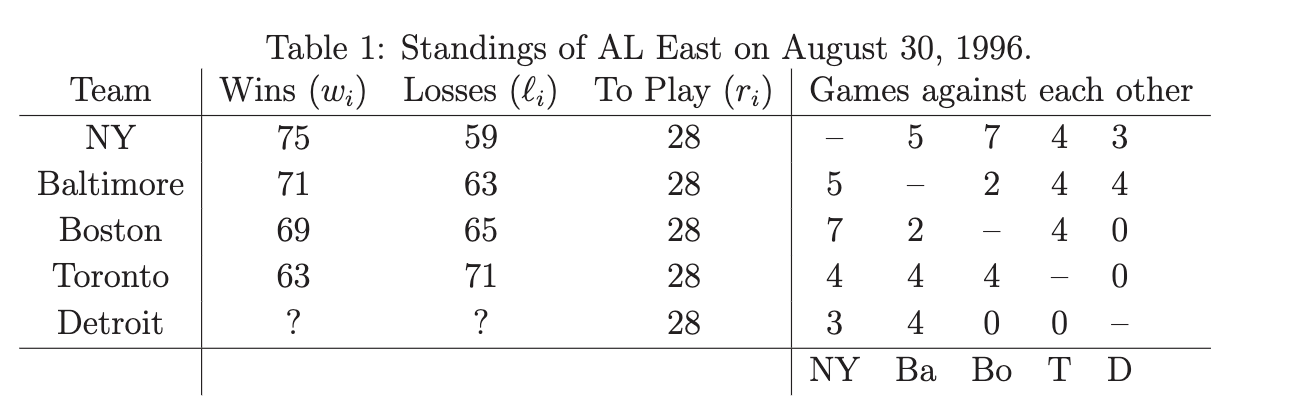
Observe that teams playing each other that can affect the outcome.

  • If w5 = 46, Detroit is eliminated. What if w5 = 47, w5+r5=75 = w1, Detroit is still eliminated. Because w5+r5+max(winning) = 54+r5, w1+r1+min(winning) = w1+r1. Either Baltimore or Boston will win by w3+r3+ # games NY loses to Boston = 76+r3
  • What if w5 = 48? Edge cases are complicate to analysis

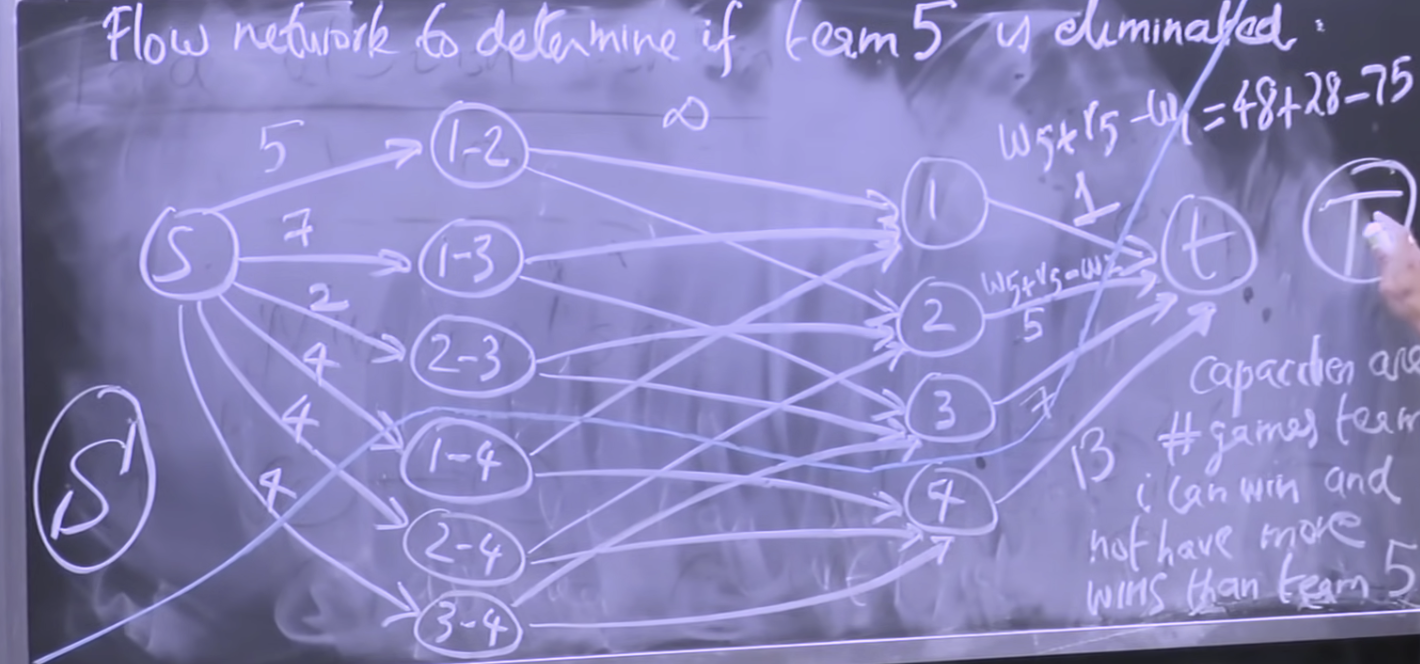
Analysis: convert tables/data to flow network (frame of translation)

  1. add capacities to v-t edges such that max flow represents elimination
    • c(v, t) = w5+r5-wi, # games team i can win and not have more wins than team 5
  2. Intuition: Assume team 5 wins all remaining games. Divvy up remaining games (sending flow through these edges). All teams have <= w5 + r5 wins (=> team 5 is not eliminated)
  3. Find the min cut (minimal capacity): c(S, T) = 25 => elimination

4. Team 5 (Detroit) is eliminated if and only if max-flow does not saturate all edges leaving the source, i.e., max flow value < 26.

  • saturate: all the games have been played
  • Argument: If you can’t play all the remaining games without exceeding the capacity of i->t edges, team 5 is eliminated.

Proof.