6.046 greedy algorithms

Algorithms › 6.046 algorithms design

minimum spanning tree

Notions+

  • tree, connected acyclic graph
  • spanning, it contains all the vertices
  • spanning tree of graph G is the subset of edges of G that form a tree & hit all vertices of G
  • E, undirected edges
  • The fastest MST is a randomized algorithm with O(V+E) proposed by KKT in 1993

MST: given graph G=(V, E) & edge weights w for E , find a spanning tree T of minimum weight .

Goal: exponential # spanning tree -> polynomial (geedy) -> near linear time

greedy properties

  1. optimal substructure: optimal solution to subproblems -> optimal solution to a problem
  2. greedy choice property: locally optimal choiced lead to a globally optimal solution

optimal substructure for MST

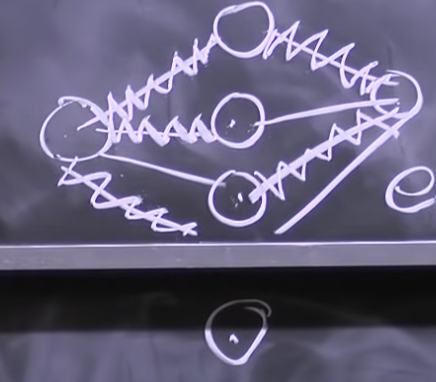
If e = {u, v} is an edge of some MST:

  1. remove edge e: still connected by red lines, not working

  2. contract e: merge u,v, contraction preserves connectivity.

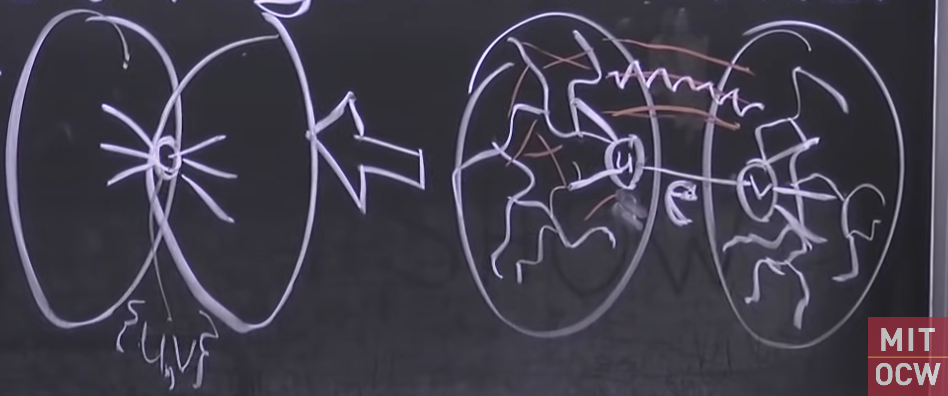
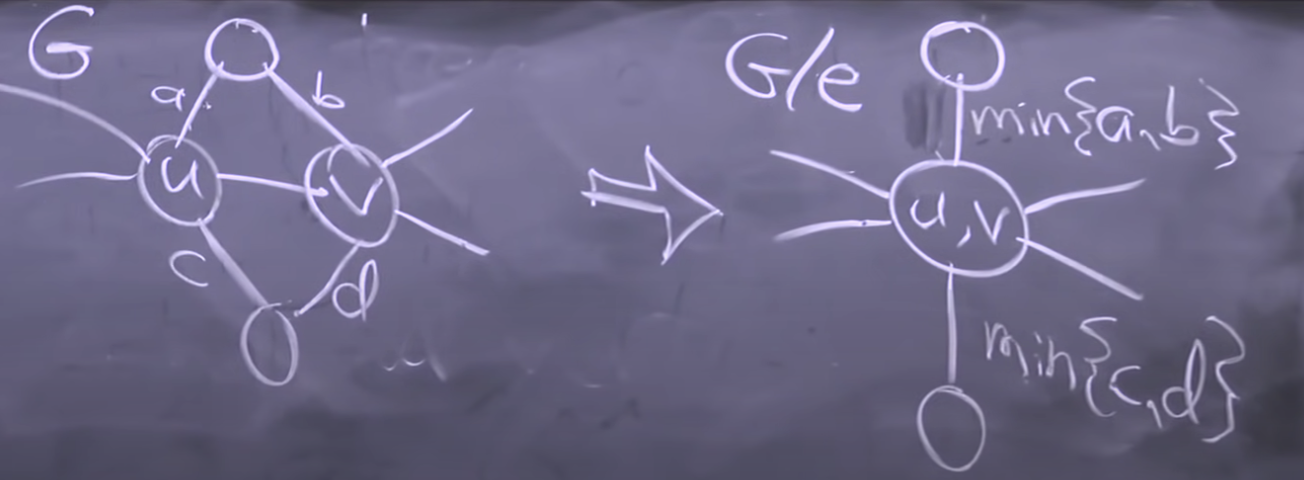
1. If T’ is a MST of G/e, then T’ {e} is an MST of G.

Proof. Say e MST T* & G

  • => T*/e is a spanning tree of G’ = G/{e}, by connectivity.
  • T’ is an MST of G’ =>
  • =>
  1. DP algs: Lemma 1 prove the correctness of this algorithm
    • guess edge e in a MST
    • contract e
    • recurse
    • decontract e
    • add e to MST
  2. analysis: reduce exponential time by taking a good guess

greedy choice property for MST

  1. cut and paste argument for greedy proof
    • cut (S, V-S), a crossing edge is the edge that crosses the cut
    • only modify edges crossing cut
  2. Lemma2 provides good guess

2. Consider any cut (S, V-S), S V. Say e is a least-weight edge crossing cut, e = {u, v}, u S, v V-S, then e some MST.

Proof. Let T* be a MST of G. Say e T* (modify T* to include e).

  • => there must be e’ T* crossing the cut.
  • is spanning tree (graph theory)
  • greedy part:
  • => is MST

Prim’s Algorithm

  1. Idea: choose a cut - a single vertex, an arbitrary start vertex s. And find the minimum weight edge sequentially to connect all vertices. Return our MST.
  2. Design: maintain priority queue Q on V-S where v.key = min{w(u, v) | u S}; Choose arbitrary start vertex s ∈ V, s.key = 0
  3. Proof for correctness
  4. Analysis:
    • O(E) results from the sum of # of adjacent vertices in G, which is 2|E| by the handshaking lemma

Invariants of Prim’s Algorithm are:

  1. v S => v.key = min{w(u, v) | u S}
  2. Tree within S MST of G

Proof of 2.

Kruskal’s Algorithm

  1. Idea: take the globally lowest-weight edge and contract it.
  2. Design: Maintain connected components that have been added to the MST so far T, in a Union-Find structure
  3. Proof for correctness
  4. Analysis:
    • Union-Find data structures
    • If w in [0, E^O(1)], using counting sort or similar can make Kruskal’s beat Prim’s
1
2
3
4
5
6
7
Initialize T = 0
for v in V: Make-Set(v)
Sort E by weight
For e = (u, v) in E (in increasing-weight order):
    if Find-Set(u) != Find-Set(v):
        Add e to T
        Union(u, v)

. The tree-so-far T MST T*

OLC

  1. exponential number of edges to guess that form the MST.
  2. handshaking lemma is sum of in-degree vertices and out-degree vertices are both |E|