6.046 augmentation
The main idea of augmentation is to modify existent (off-the-shelf) data structures to store additional information.
Easy tree augmentation¶
Goal: store x.f (subtree rooted at x) at each node x
Theorem: Suppose x.f can be computed (updated) in O(1) time from x, children and children.f. Then, modification a set S of nodes costs O(# of ancestors of S) to update x.f.
- updating x means to walk up the tree to the root
- Doing a logn rotation spreading out will likely cost O(log^2(n)) time. Because the sum of ancestors may be O(log^2(n)), whereas a single path in easy trees taking O(logn) time as AVL tree and B 2-3 tree.
Order-statistics trees¶
Goal: design an ADT interface that supports insert(x), delete(x), successor(x), rank(x), select(i)
Rank(x): find x in sorted order
Select(i): find the element of ith rank
Idea: rank(x) = # elements of all that is less than x + 1. Walk up the tree to the root and recursively calcutate x’.left.size + 1(depending on the initial index) where x’ is less than x.
Select(i) takes advantage of special case of rank(x) to avoid recursive calls. The rank of root x is equal to x.left.size + 1. Then just walk down the tree and search ith element.
Problem: why not store ranks or depths (count down from the root) of nodes into the tree?
Shortcomings: Inserting (-inf) or the elements with decreasing order to the tree will cost linear time to update the augmented information. The rank of every element goes down by one. Meanwhile, the depths of nodes are hard to maintain due to rotations affecting most nodes. Height(x) is not affected by that because the distance from root to x is not changed.
Finger search trees¶
More sophisticated operations are involved.
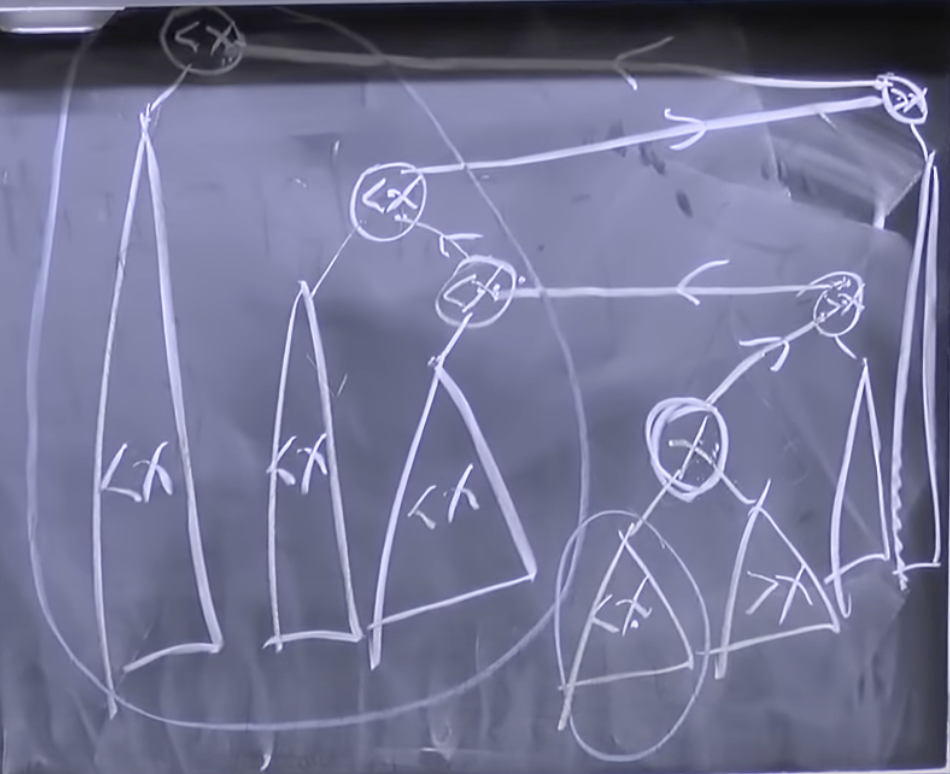
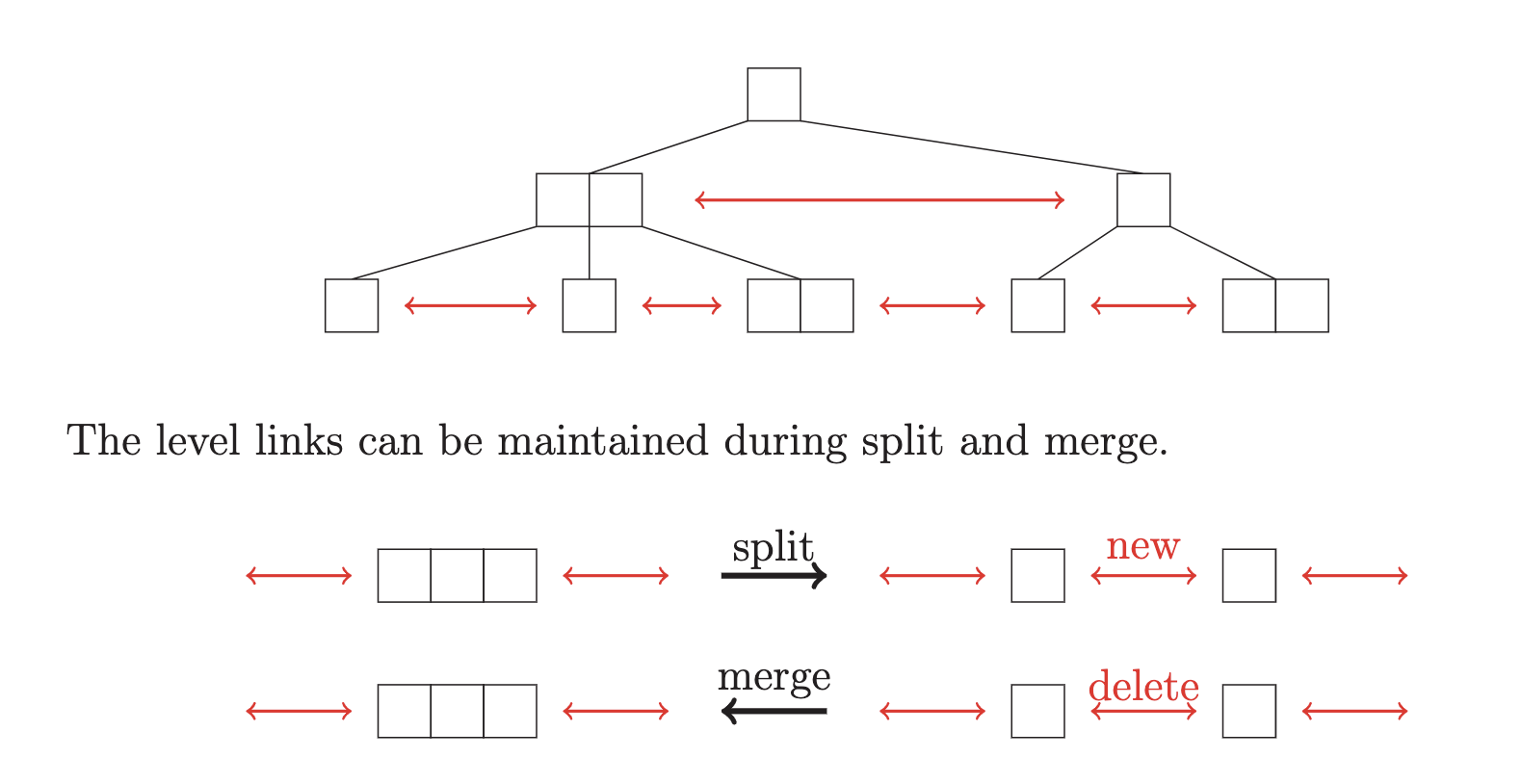
Idea 0: Level-linked 2-3 trees.
Level linking¶
store Left -> Right & Right -> Left pointers for each nodes. => Easy to maintain in constant time
Finger search property: expect searching x nearby y after searching y to run fast. => constant time + worst search time O(logn)
Search (x from y)¶
problem 1: how far it achieves?
- idea 1: log difference of ranks, O(log|rank(y) - rank(x)|= O(log(k))
- distance from x and y, varying in different data structures where b tree has level length and bst does not.
Problem 2:
in 2-3 tree, x is y’s predecessor with constant rank difference and logn height, thereby it’s incorrect to use log difference of ranks of nodes.
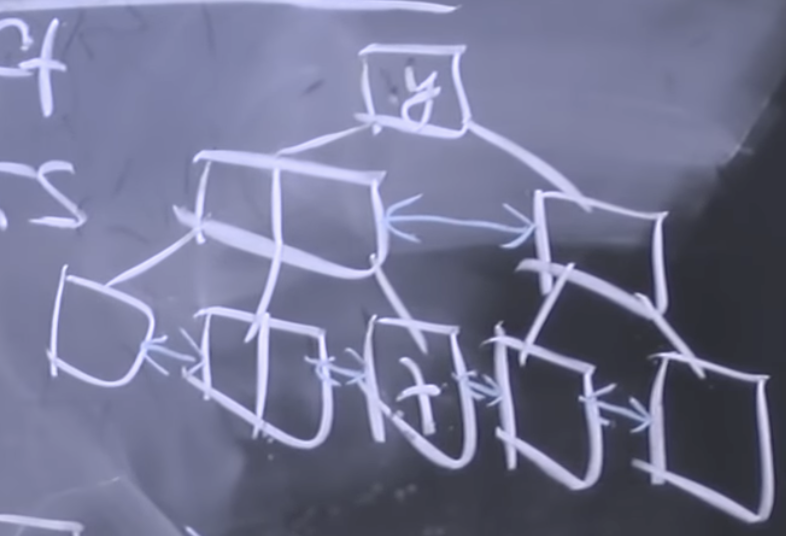
Data in the leaves¶
Idea 2: store data in leaves.
b tree, bst tree: put one key in one spot
b+ tree: put keys only in leaves. Most info is originally stored in leaves by space. Others else are the same as b tree.
Search: augment to store min & max of subtrees
Insert: split and merge

Initialize v to the leaf node containing y (given), then while: xxxxxx
example: 51:00
Range trees¶
Goal: prepocess n points in d-D dimension to support query:
given box, find 1) # points in the box,
and 2) k points in the box -> theta(k) for output
=> O(log^d(n) + |output|)
1-D¶

sorted array: O(logn + k)
(not balanced) BST: O(logn + klogn)
level-linked b tree: O(logn + k)
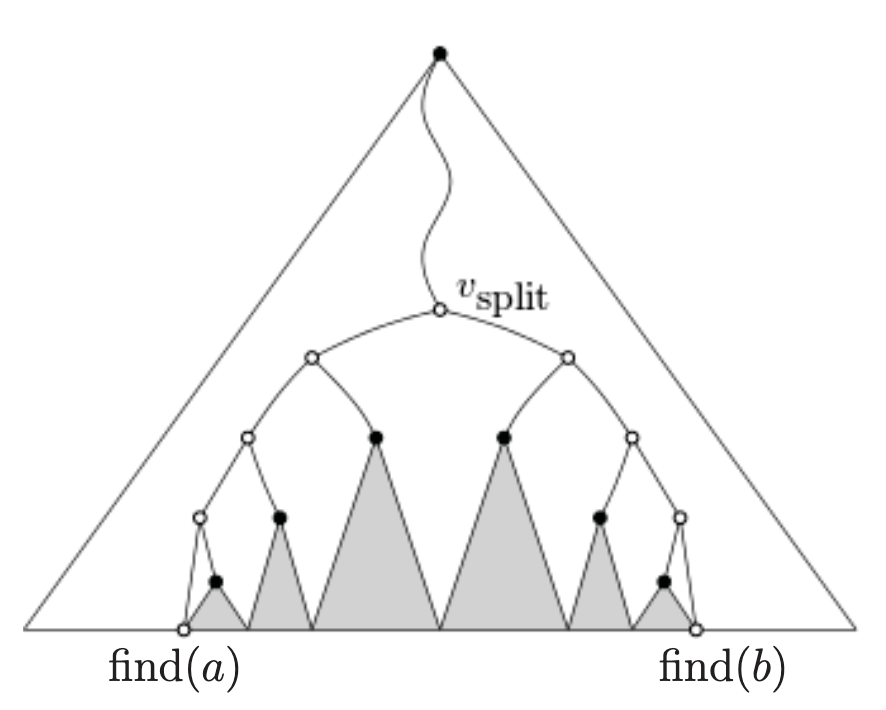
1-D range tree: perfectly balanced BST (AVL) => O(logn + k)
Range-query(a, b): find the least common ancestor (LCA) of a and b and return the nodes and the root nodes of subtrees “in between”
Notes:
- node and subtree of that node
- left parent, right parent
Orthogonal range searching¶
2-D case: Fixed y, project (x, y) to the x axis as range tree. Then the problem becomes range-search(a, b) in 1-D range tree just like before, thereby doing another 1-D range tree searching on those points projecting to the y-axis to solve it. d-D case can be done by nested searching in the same manner.
space complexity: each key k lives in O(logn) rooted subtrees which are all the ancestors of k.
- It means total space is O(nlogn). In d dimensions, O(nlg^(d−1)n).
-