6.046 dynamic programming

Sam Li

2023-01-25

Algorithms › 6.046 algorithms design

Introduction
Basic
- Rectangualar blocks
- Longest Palindromic Seq
Medium
- Optimal BSTs
- Alternating Coins Game
All-Pairs Shortest Paths
OLC

DP notion:

Characterize the structure of an optimal solution
Recursively define the value of an optimal solution based on optimal solutions of subproblems
Compute the value of an optimal solution in bottom-up fashion (recursion & memoization)
Construct an optimal solution from the computed information

Introduction¶

The main idea of dp: subtract and solve the subproblem, then reuse the results

Runtime: the number of unique problems+ the amount of merge work

In the recitation, a simple dp example is to solve the number of unique paths from (1, 1) to (M, N).

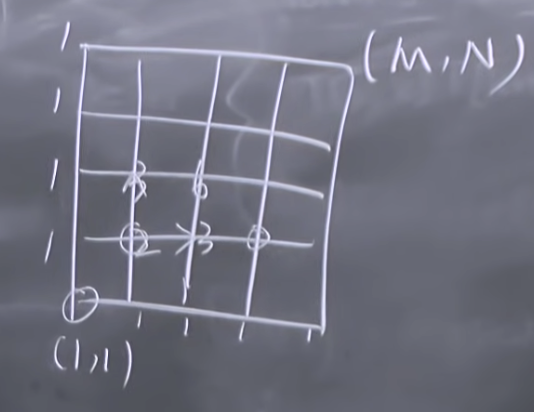
Subproblem: To the points on the edge, just one path; to the middle points, path to the left point + path the right point
Runtime: # subproblems = O(MN)
olc: I misunderstood that the subproblems should start from (M-1, N-1) -> (M, N) which makes solutions hard to get.

Make change example: Make changes for N cents. There are 1=S1 < S2 < … < S_M cent of coin. Find the minimal number of coins needed.

Subproblem: do a exhaustive search. Pick Si, then MC(N) = min{1 + MC(N-Si)}. N > maximum of subproblems of min{MC(N-Si)}
Runtime: O(MN).
It’s similar to knapsack problems (NP-complete). The linear solution here is due to the size of input is log(N), thereby it’s still exponential.

Basic¶

Rectangualar blocks¶

problem: A set of n blocks, {1, 2, …, n}, l_i, w_i, h_i. J on top i, require l_j < l_i, w_j < w_i. Rotating not allowed. Find the maximum height.

? RB(1, 2, …, n)

olc: the subproblem is whether to put the next block j on top of current (j-1) blocks.

Rec:

Approach 1: exhaustive search

RB(1, 2, …, n) = max{h_i + RB(…except i…)} -> messy constraints l, w
redefine a compatible set C, then RB(1, 2, …, n) = max{h_i + RB(C_i)}
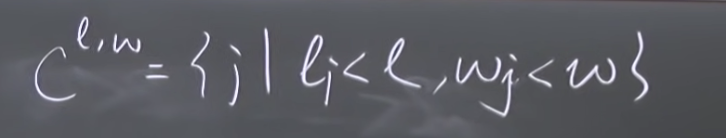
Runtime: O (n^2), # subproblems = n.
- what’s in the compatible sets C? How to find C?
  - O(n^2): Scan the entire set, find the minimum for each one
  - O(nlogn)?

Approach 2: weighted interval scheduling

Sorted by length and then width {1, …, n}

RB(1, 2, …, n) = max{(h1 + RB(C_i)), RB(2, …, n)}

Runtime: O(n), # subproblems = n; + O(nlogn), sort; + O(n^2)/O(nlogn) find C set.

Longest Palindromic Seq¶

Input: a sequence of letters -> a string X[1…n], n >=1

Output: (limits) answer >=1

Strategy: L(i, j) is the length of longest palindromic subsequences of X[i…j] for i <= j.

X = 'underqualified'
n = len(X)
Dict = [[0 for _ in range(n)] for _ in range(n)]
def L(i, j):
	if (Dict[i][j] != 0): # memoization
		return Dict[i][j]
	if i == j:
		Dict[i][j] = 1
		return 1
	if X[i] == X[j]:
		if i + 1 == j:
			Dict[i][j] = 2
			return 2
		else:
			return 2 + L(i+1, j-1)
	else:
		Dict[i][j] = max(L(i+1, j), L(i, j-1))
		return Dict[i][j]

for i in range(n): print(Dict[i])

Problem 1: How to trace backwards to generate output sequence?

ChatGPT: use dp array to trace back and print the result.

def printLPS(i, j):
    if i > j:
        return ""
    if i == j:
        return X[i]
    if X[i] == X[j]:
        return X[i] + printLPS(i+1, j-1) + X[j]
    if Dict[i][j-1] > Dict[i+1][j]:
        return printLPS(i, j-1)
    return printLPS(i+1, j)
print("Longest Palindromic Sequence: ",printLPS(0, len(X)-1))

Problem 2: How to write dp iteratively?

Iterating: solve subproblems in order of increasing j − i so smaller ones are solved first

Analysis: # subproblems * time to solve each subproblem

Suppose X[i] are distinct, T(n) is running time on input of length n, T(n) = 2^(n-1)
- 1, n=1
- 2T(n-1), n>1
But there are only C(n, 2) = distinct subproblems: (i, j) pairs with i < j.
Given that smaller ones are solved, lookup is O(1)
memoizing, hash, lookup hash table or recurse

Medium¶

Optimal BSTs¶

Given: keys K1, K2, …, Kn, K1 < K2 < … < Kn, WLOG Ki = i

weights W1, W2, …, Wn (search probability)

Find BST T that minimizes: , which is minimizing expected search cost. Frequently accessed keys are closer to the root and thus accessed faster.

BST invariant: e(i, j) = cost of optimal BST on Ki, K_(i+1)…, Kj. Then the subproblems are {sets < Kr} and {sets > Kr}.
Want e(1, n).

Enumeration: draw trees when n=2, 3

Greedy solution?: Pick Kr in some greedy fashion, e.g., Wr is maximum. Use the key with maximum Wr as root node.

Greedy heuristic: the maximum weight node should have absolute minimum depth.
Why greedy does not work?
- Intuition: when the maximum weight node happens to be Kn, the tree is highly unbalanced with all the nodes on the left of root node.
- Nick Davis ex: Kn = 4, weights: 1, 10, 8, 9

DP solution?:

First question: what is the root node? Guess!
- Make a linear number of guesses corresponding root node
- e(i, j) = e(1, r-1) + e(r+1, j), one level below e(i, j)
- e(i, j) =
  - wi, if i = j
  - MIN(e(i, r-1) + e(r+1, j) + W(i, j)), i<=r<=j
- W(i, j) is sum of the weights from i to j. The weights add up when it goes deeper in recursion.
Complexity: . When j-i = 1, e(i, j) is certain and that makes up of C(n, 2) pairs.

Alternating Coins Game¶

Question: Row of n coins of values V1, … , Vn, n is even. In each turn, a player selects either the first or last coin from the row, removes it permanently, and receives the value of
the coin.

Can the first player always win? ->Guaranteed not to lose
Try: 4 42 39 17 25 6

Strategy?

Compare V1+V3+…+Vn-1 against V2+V4+…+Vn and pick the greater one
only pick from the chosen subset during the game

Problem: maximize the amount of money won for the player moving first?

Optimal Strategy: assume the opponent always pick best move for it -> modeling in the middle

V(i, j): max val the player can win if it is its turn and only coinds Vi, …, Vj remain. V(i, j) =
- V(i, i), pick i (model the opponent behavior)
- V(i, i+1), pick the maximum of the two
- V(i, i+2), V(i, i+3), …
V(i, j) = max {pick Vi, pick Vj}
- complication: V(i+1, j) is not the board in front of the first player that it can control. It should be the board that gets back after the opponent moves.
- max {<range (i+1, j)> + Vi, <range(i, j-1)> + Vj}
V(i+1, j) subproblems with opponent picking
- min {V(i+1, j-1), V(i+2, j)} Vs. the opponent picks Vj or Vi+1
- Certain.
V(i, j) = max{min{V(i+1, j-1), V(i+2, j)} + Vi, min{V(i+1, j-2), V(i+1, j-1)} + Vj}
Complexity:

All-Pairs Shortest Paths¶

Notations+:

edge-weighted graph, G = (V, E, w)
is the weights from u to v
Dijkstra for SSSP: O(E + VlgV)
assume w(u, v) = if (u, v) E
E = in sparse case
Bellman-Ford analysis to detect no negative cycles: no negative

Question: given G = (V, E, w), find for all u,v V

Simple solution: APSP = run SSSP for each of V = |V| * Dijkstra
Johnson’s algorithm beats general Bellman-Ford and achives the general Dijkstra complexity bound.

Goal: achieve first and then

DP1¶

subproblems: = weight of shortest path u->v using <= m edges
guess: WLOG, guess last edge (x,v)
recurrence: = for x V)
- base case: = 0 if u =v; otherwise
acyclic (tological order): for m = 0, 1, …, n-1: for u and v in V:
original problem: if no negative cycles, then = = = … (In the worst case, traverse through all vertices without revisiting any vertex)

Analysis

relaxation step is: if then
Complexity: , no better than general Bellman-Ford
relaxation step can be: = for x V) with overall running time of time

Matrix multiplication¶

standard matrix multiplication computes , both n*n matrices.
The fast running time is comparing to standard algorithm being
connection to shortest paths:
- define = min, = +, , , V = {1,2, …, n}
- computation: semiring is * and +
- complication: is circle-multiplication of W with itself m times
- complexity:
optimize matrix multiplication: repeated squaring
- ( ( )^2 )^(2…) = , mutliplied by times
- assume no negtive cycles, complexity is , better than general Bellman-Ford
transitive closure: = 1 if path i->j; 0 otherwise.
- = OR, = AND
- for dense graph is best

DP2, Floyd-Warshall algorithm¶

subproblems: = weight of shortest path u->v whose intermediate vertices {1, 2, …k}. F-W insight on 70s
guess: is k the path
recurrence: =
- base case: , not to use any intermediate vertices
acyclic: for k: for u and v in V:
original problem: = . Negative weight cycle is negative

Analysis

complexity: , compared to DP1the guessing time is constant and same # of subproblems.

Johnson’s algorithm¶

idea: change weights on edges so no negative weights exist, then run Dijkstra on it. Translate to old weights and get the result.
steps
- find h: V -> R such that for all u,v V.
- Run Dijkstra on (V, E, ) from s V => get for all u,v V
- Compute by
Proof of correctness: the shortest path is preserved but offset.
Analysis:

Proof. For any u->v path p in the graph G, say p is v0 -> v1 -> … ->vk, where v0 = u and vk = v.

$§$

Hence …

Problem: How to find the weight function h?

triangle inequality: for all (u, v) in V, called a system of difference constraints
application: can think as an event v is happening before event u with constraint w

1. If (V, E, w) has a negative-weight cycle, there exists no solutioon to the above system of difference constraints.

2. If (V, E, w) has no negative-weight cycle, then we can find a solution to the difference constraints.

OLC¶

Bottom-up starts with the smallest subproblems first and build up to larger subproblems. Top-down starts with the original problem and breaks it down into smaller subproblems.
Bottom up via relaxation means solve subproblems by relaxing edges.
DP guess is linear.