hw2 graph
ps5¶
BFS
1 | # BFS |
Analysis:
-
overall runtime of this BFS: O(|V| + |E|) or O(|E|)
- inner loop takes O(|E|) time: it cycles through all deg(v) outgoing edges from vertex v.
- Parent has length |V|
-
Graph radius
-
network
Approach: construct a graph.
Idea: add an additional node s (a super node) to the graph with an edge to every entry point.
-
search for connected components
ps6¶
DFS
-
topological sort: DAG
- Simple graph has no self-loops, DAG has no loops
-
relaxation
- Tree: In a tree, there is a unique simple path between any pair of vertices, as two distinct simple paths could be used to construct a cycle.
-
DAG relaxation
-
Bellman ford: detect loops and negative weight
-
Input
-
DAG problem
-
Use DFS to check visiting order is the particular topological order
-
Topological tree has no backward edges/loops.
-
Auxiliary information: index
-
ps7¶
- Feel smooth when thinking it as water flow.
- How pq breaks ties may change the visiting order
- It should be clear how to implement operations.
- think about connected components (这个图的减小的方式是通过扔掉已经确定是最短路径的点来进行的
- negitive weights: detect negative loops
- connected component C: one vertex can reach any vertex
- we don’t know if the graph is connected. Likewise, it should be considered if a graph is a DAG/connected/weighted/…(graph’s property)
- how to find a connected component: considering it is a undirected graph, use DFS/BFS to find C.
- Whether has negative loops
- Yes, V in C is -inf, V not in C is inf
- No, use Dijkstra
- connected component C: one vertex can reach any vertex
Recitation¶
Terminology:
- Bipartite graph: a graph whose vertices can be divided into two disjoint and independent sets U and V, that is, every edge connects a vertex in U to one in V.
- DFS search: search a graph from a specific vertex or an entire.
- DAG: A directed graph containing no directed cycle is called a directed acyclic graph or a DAG
- Topological sort: in a DAG G=(V, E), a linear ordering of the vertices such that for each edge (u, v) in E, vertex u appears before vertex v in the ordering.
The problem solving process: transform raw input to IN, apply the algorithm we are familiar with, read raw output to OUT.
Then calculate the runtime and prove for correctness and efficiency.

BFS¶
level sets L_i is the set of vertices reachable from s via a shortest path of length i. Breadth-first search discovers levels in increasing order starting with i = 0 where L_0 = {s}
DFS¶
Relaxation: search for a solution to an optimization problem by sorting with a solution that is not optimal, then iteratively improves the solution until it becomes an optimal solution to the original problem.
Think of the initial distance values as being very “tight” or “constrained” (e.g., initialized to infinity), and relaxation as loosening the constraint when a shorter (better) path is found
- delta (s, v): weight of the shortest path
- d (s, v) = +inf (except d(s, s) = 0)
- if d(s, v) = delta (s, v), d(s, v) fully relaxed
How to relax? And when to stop relaxing?
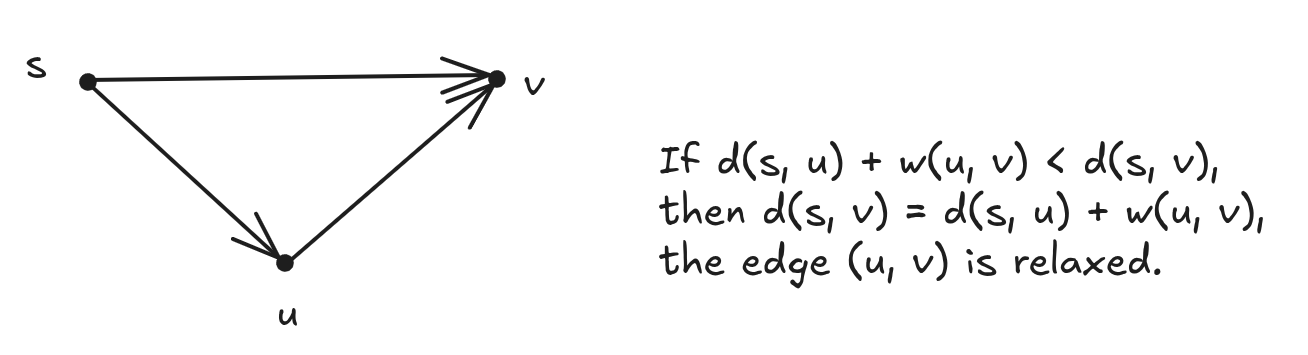
The definition of topological sort depends on the acyclic property of DAG.
The important part is reasoning process so that we can reason by ourselves to get the answer
edge classification
- tree edge(DFS traverse)
- not tree edge
- Back/forward/cross edge
Problem 1: how this concept relates to DFS?
Problem 1.1: how that defers to undirected graph compared with directed graph?
topological sort -> directed, acyclic, graph
Problem 2: how this concept relates to topological sort?
Weighted graph¶
problem 0: how to build a shortest path algorithm?
simple case: take an edge, split it up, put in fake nodes. Then use BFS
Problem 1: shortest path with odd edges?
比较有趣的是可以把两个状态看成两个平面。
Idea: track state during path building
problem 2: fast way, least fuel. An edge has a fixed fuel cost and a varying time cost, depending on the time table Tc (in minutes), where M = 24 × 60
Idea: choose a more reasonable state to track and reason carefully.
Bellman-ford¶
Notice: negative weight
-> detect loops
Dijkstra¶
Notice: non-negative weight
讲义中分成两部分来看这个算法。整体上看: Dijkstra 像一个流动的水龙头阀门,水流从起点匀速地流动到下一个开关。算法把连续的过程通过 edge relaxation 离散的表示。
-
Edge relaxation: priority queue -> extract_min/insert/delete
-
算法的运行时长与 pq 的具体实现有关。可以从三种角度看:
存一对 (key, value), 需要实现三个操作。
- 当图的点密集时:|E| = Ω(|V|^2) ; direct_access_array; T = O(|V|^2+ |E|)
- 当图的点稀疏时:|E| = O(|V|) ; heap; T = O((|V |+ |E|) log |V |)
- 介于两者之间:binary heap; T = O(|V |log |V |+ |E|)
All pairs shortest paths¶
Runtime: at least O(V^2), because we need find all pairs’ path
naive approach: use n * SSSP algorithms:
- Using Dijkstra for each vertices so as to solve APSP is easy to think but has details to rethink.
Better:
tricky part: how to deal with negative weights?
-
adjusting edge weights
problem 1: Are shortest paths still shortest paths?
- it’s easy to think of adjusting edge weights by adding a large number to each edge weight. But it will base paths with fewer edges.
- Idea: pick a node u, add 10 to its incoming edges, and subtract 10 from its outgoing edges.
Problem 2: it’s hard to think a general reweighting functions.
-
making all wights nonnegative
Clever choice of reweighting function: Add a new node X with weight-0 directed edges (X, v) for each v ∈V , and choose h(v) = d(X, v).
-
Johnson’s algorithm is basically two parts: reweighting function then n * dijkstra.
-
the essense is the way to construct a new graph G’ with nonnegative weights:
Add new vertex X and weight-0 edges (X, v) for all v ∈V as above, and run Bellman-Ford from X to compute h(v) = d(X, v)
-
make sure changing back to G.
The correct d values in G are d(u, v) = d′(u, v) + h(v) −h(u), and the shortest path trees in G′are also shortest path trees in G
-
olc¶
-
I think the basic idea is data transformation and build intuition about the problems.
-
why should we know about edge classification…? because it would help to understand the problem better.
-
Lec 14 notes (19fall) about APSP is worthy reading.
-
Relaxation: it checks for (u,v) in constructing graph
-
python lambda expression
1
lambda x: x**2
-
Why doesn’t Dijkstra’s algorithm work with non-negative edge weights?
I think the tight bound is Dijkstra not allowing negative loops that will destroy its minimal property.