hw1 data structures

Algorithms › 6.006 algorithms

ps2

  1. 看题：when all but one is special means only one is not special.

  2. set view and sequence view of data structures

    • Sequences maintain a collection of items in an extrinsic order, where each item stored has a rank. In the sequence, including a first item and a last item. That the first item is “first” is because some external party put it there.

    • By contrast, sets maintains a collection of items based on an intrinsic property involving what the items are, usually based on a unique key, x.key, associated with each item x.

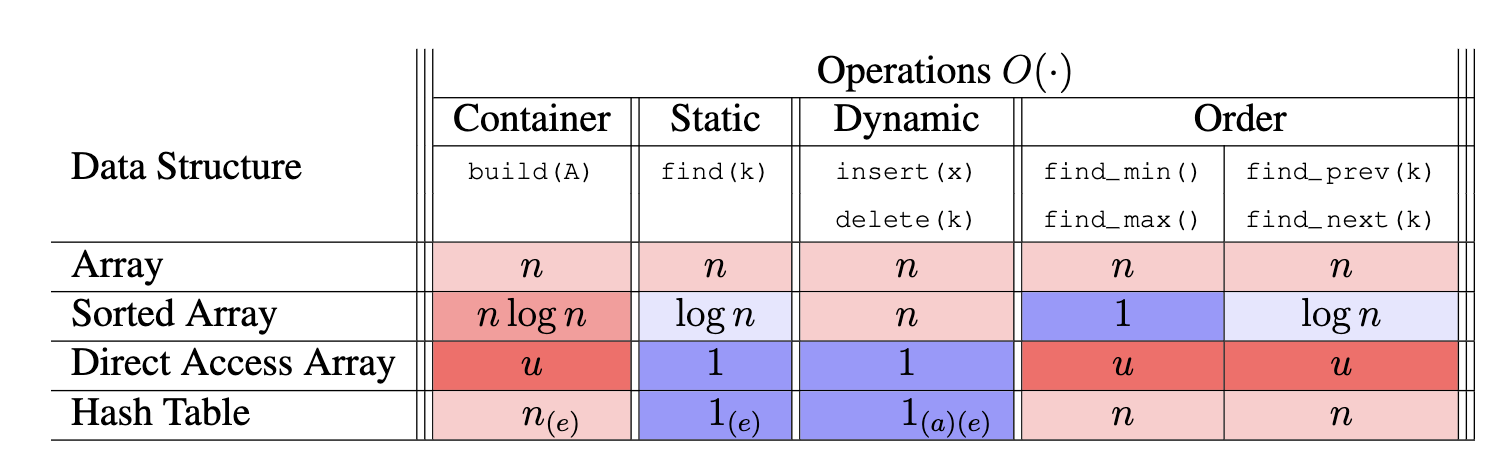
    Set: hash table, binary search tree

    Sequence: array, linked list, direct access array

    That’s why sequence has insert/delete_at_somewhere operations while set has a loosen insert/delete items operation and supports order operations to find the items.

  3. Merge_sort

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    def merge_sort(Arr):
    	size = len(Arr)
    	if size == 1:
    		return Arr
    	mid = size//2
    	Left = merge_sort(Arr[:mid])
    	Right = merge_sort(Arr[mid:])
    	i,j = 0,0
    	start = 0
    	while start < size:
    		if j >= len(Right) or (i < len(Left) and Left[i] < Right[j]): # offbyone error
    			Arr[start] = Left[i]
    			i += 1
    		else:
    			Arr[start] = Right[j]
    			j += 1
    		start += 1
    	return Arr # missing return value

ps3

  1. How to use hash tables(its set operations) to implementing sequence operations?

    Read the problem. We are not storing things in order but storing in hash tables.

    idea 1: assign key to each item as index

    • Seq[key] = value

    • Seq-build(A): set-build(<key, A[i].value> for i = 0,1,2,… )

    • insert/delete_at: iterate all items, insert/delete one, rebuild

    • Insert_last: easy, however insert_first would take linear time

    Idea 2: have an extra varibles to track the original index

    • How many index should we track at least?

      one: First

        • Store variable first = key of first item(index 0)
        • Hashing(map negative index to positive)

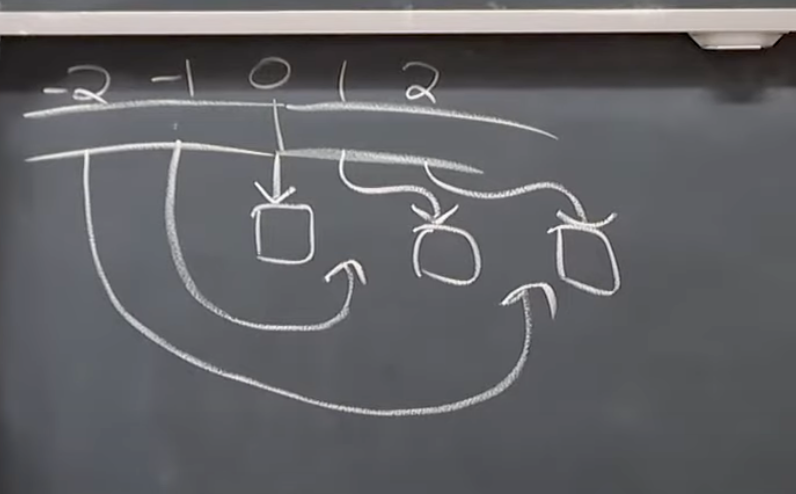
      • Insert_first: decrement first, insert(<key first, value x>)

      • and make tiny fix to previous operations(ex: find(i+first))

  2. best sorting algs: sort n objects by keys

    nagative items: Increase a large enough number then sort. Decrease after sorting.

    String: convert str to a unique number and use radix sort

    Number of fignts fought: counting sort is enough. Or merge sort.

    ratio w_i / f_i (w_i < f_i): it’s a floating number. We need to consider the precision

    Idea: mapping rational number/letters/negative integer to integer

    runtime of radix sort is O(n + nlog_n_(u)), such that it can handle any polynomial u.

    突然想到了data-oriented pattern

  3. college construction

    1. naive approach: check for h - s_i for S_i, this would take O(n**2) time

    • problem: how to speed up to O(n)?

      • use data structures: store the input S in hash table S’: we can search (h - s_i) in S’ for si in S, each find take O(1) time.
    1. h = 600*n**6, add two things up.

    Idea 1: radix sort

    • naive approach: store S in sorted_array_set where sort method is implemented using radix sort. For any S_i, binary search for (h - S_i) in S(know as find_prev).
      • It takes O(n*logn) time

    Idea 2: two-finger algorithm

    • Improvement 1: linear scan: any S_i greater than h is impossible. Rebuild S’ in the sorted_array_set where S’_i < h.
    • Improvement 2:

  4. copy detection problem

ps4

binary tree

Problem 1: why we need a binary tree to store items?

ans: Compared with linked list which takes O(n) time to traverse all the items, we use binary serach instead. The traverse now takes O(hight of the tree) = O(logn) time.

Design:

  1. We define the traverse order to meet our needs.

    • we can use binary tree to implement sequence(order) or set…
    • property: represent binary relation in different way: left-aligned complete binary tree

  2. Navigation: first/last, walk down/up the tree

  3. Dynamic operation: add or remove items in a binary tree

    problem 2: maintain the tree balance while insertion/deletion

    The logic is that if skew is not in the balance range(-1,0,1) in such condition it changes into (2,-2), we should rebalance the tree. First, we need to detect such conditions, then we should modify that by rebalance(namely, by rotations). After each rebalance operation, we need to update the subtree heigh to calculate update skew. Then we walk up the tree and maintain balance in each recursion step until there is none.

    • Rotation

      Problem 3: what will happen after rotations?

      just draw the picture.

      • Rotate right(D): D becomes its left child’s right child, and subtree_update
      • Rotate left(B): B becomes its right child’s left child, and subtree_update

    觉得讲义上的insert B before A有点怪

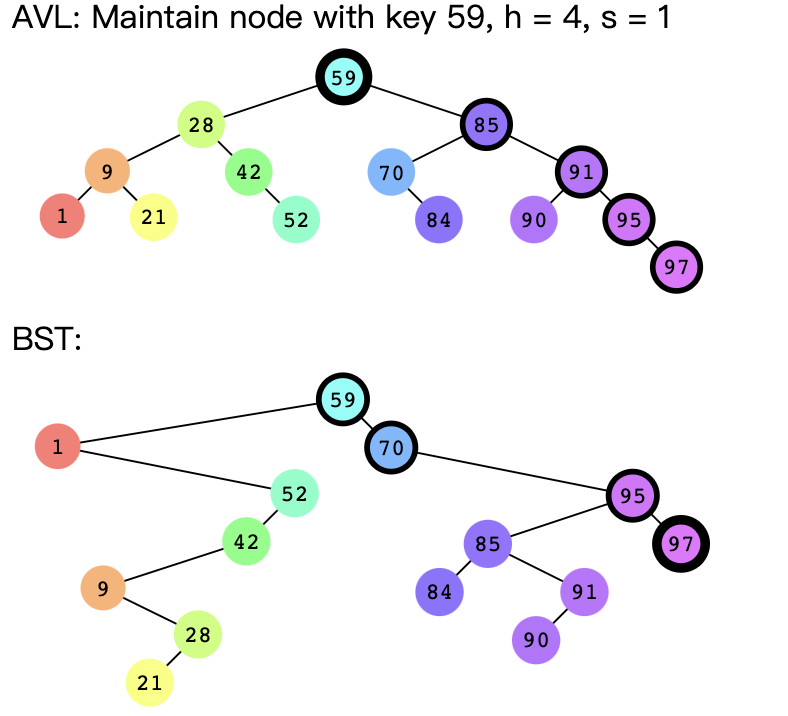
    Problem 3: BST and AVL have nuances in insertion/deletion.

    这一点我看错了，我把插入节点的大小搞错了，这两个树结构的差异是由于AVL会维持树结构的平衡。

    BST: deletion: swap down predecessor/successor

the difference between BST and AVL is: AVL maintains balance: AVL will check skew of every node in the traverse order to decide rotation operations; BST mains binary search.(AVL can use binary search as well)

heap

Build heap in linear time:

  • idea: walk up the heap.

    -> loop backward over array.

    problem: the order of swapping

heap doesn’t support ordering.

problem set

  1. n items, k largest one list. O(logn) space to write, O(nlog(logn)) runnning time.

    Problem 1: how is logn related to k?

    这两个题目不一样😅，这道题根本没提到k。解法和我之前想的一样

  2. SCLR: 设计一个数据结构满足：

    new_bid(d,b), O(logn);

    update_bid(d,b), O(logn);

    get_revenue(), O(1).

    we should ask ourselves these questions before writing down the answer:

    • what is stored in data structures? ->
    • what is maintaining by operations? ->
    • what is querying? ->

    Idea 1: we should maintain a dictionary of (bidder ID, bid) for the update operations. Dictionary can be implemented by AVL tree set or hash table while the latter’s running time is amortized

    Idea 2: we need data structures to preserve the priority we need

    • naive approach: use binary heap/AVL tree
    • Store n items in one max-heap -> store k largest items in min-heap, n-k items in max-heap, in which case it doesn’t need to use delete_max to find the minimal item in max-heap.

    Idea 3: we need to link two data structures to support fast find.

    Approach: we want to find the bidder’s current bid quickly. -> cross linking

    • That’s why we don’t save bid directly in the dictionary, in which case we save the time in updating the dictionary every time we change the bidder’s bid.

  3. It seems right but where goes wrong?

    这部分看了又看,仍旧没发现错误在哪里。后来把问题定位到了一个测试进而找到了问题。忽略了max_temp是所在class的instance，所以在bug版第一个判断语句永远都会返回None.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    # bug
    def subtree_max_in_range(A, d1, d2):
        max_temp = None // # fixed by changing all max_temp to another name like temp
        # ------------------------------------ #
        if A.max_date <= d2 and A.min_date >= d1:
            return A.max_temp
        if A.max_date < d1 or A.min_date > d2:
            return None
        if d1 <= A.item.key <= d2:
            max_temp = A.item.temp
        if A.left:
            l_temp = A.left.subtree_max_in_range(d1, d2)
            if l_temp:
                if max_temp:
                    max_temp = max(l_temp, max_temp)
                else:
                    max_temp = l_temp
        if A.right:
            r_temp = A.right.subtree_max_in_range(d1, d2)
            if r_temp:
                if max_temp:
                    max_temp = max(r_temp, max_temp)
                else:
                    mex_temp = r_temp
        # ------------------------------------ #
        return max_temp

recitation

AVL tree

full binary tree guarantees the height of O(logn)

Build a AVL tree with fewer nodes as possible -> prove h = O(logn)

why rotations -> balance -> tree search

Rotation:

1
2
3
4
5
6
7
8
9
10
11
12
13
rotateRight(A):
	# A's original parent e; A could be e's left/right child => B
	B.p = e
	if e.r == A # pointer comparison
		e.r = B
	else:
		e.l = B
	# A's original left child B => A is B's right child
	B.r = A
	(A.p = B)
	# B's original right child c => A's left child
	A.l = c
	(c.p = A)

Principle of algorithm

thinking process matters: take 30-60 minutes to think about a problem

problem 0: shifted array, find e in N sorted items shifted length of k,

  • if k is defined
  • if k is undefined, find k => find min

How to solve it?

  1. simplest solution: linear scan, O(N)
  2. in another way? shift k + binary search, O(k + logN)
  3. …

Problem 1: find kth smallest in N items in a min-heap, want O(K*logK)time

How to think about it?

  1. use min-heap: O(klogN), k times find_min in min-heap

  2. Find an O(NlogK) algorithms:

    Idea 1: cut out irrelevant layers. We have k levels of heap => O(k**2) time, given the height is O(k)

    Problem 1.1: how to cut a heap into k elements?

    Problem 1.2: how to split it up into k, (N - k) groups?

    Idea 2: maintain a max-heap of k. Iterate all items and we can get what we want

  3. think more about the process of finding the kth smallest items.

    Idea: horizon.

    Idea: augmentation: index of array

    1
    2
    3
    4
    5
    6
    7
    8
    9
    # initialize
    H, original min-heap(array back-based)
    Z, horizon
    Z.insert(H[1])
    for ith in range(K):
      ith, j = Z.extract-min
      Z.insert H[2j], 2j
      Z,insert H[2j+1], 2j+1
    return ith

Problem 2: find min(e[i,…,j]), e is a list of N items, N = 2**k

Process: pre-process, then query

How to think about it?

  1. simple idea: hash into [i,…,j], we can get H[[i,…,j],…], N**2 pair; then take min in O(N) time in each pair

    => O(N**3) time

    Improve to O(N**2) time by comparing current pair result with previous result which takes O(1) time

  2. how to spend time?

    • in pre-process: O(N**2) | O(1)
    • in query: O(1) | O(N)

  3. binary search in two halves recursively

Reminder

  1. two-finger algorithm:

  2. cross linking: by store pointers to another data structures.

  3. Proximate sorting

    An array of distinct integers is k-proximate if every integer of the array is at most k places away from its place in the array after being sorted, i.e., if the ith integer of the unsorted input array is the jth largest integer contained in the array, then |i −j| ≤ k. In this problem, we will show how to sort a k-proximate array faster than Θ(n log n)

    这里关于 insertion sort k-proximate array takes O(nk) time, heap sort takes O(nlogk)time 的讨论还挺有意思的。

  4. a general/naive approach and subsequent analysis

  5. approriate description

    • key with

      example 1: in priority queue: Key each Revenger ri with opinion si on the pair (|si|, i) to make keys unique.

  6. Worst-case, expected, amortized(dynamic operations)

olc

First we should decide which view:

  • ordered or not -> sequence/set view
  • does it have priority? -> priority queue -> binary heap/ binary tree