6.046 divide and conquer
Interval scheduling¶
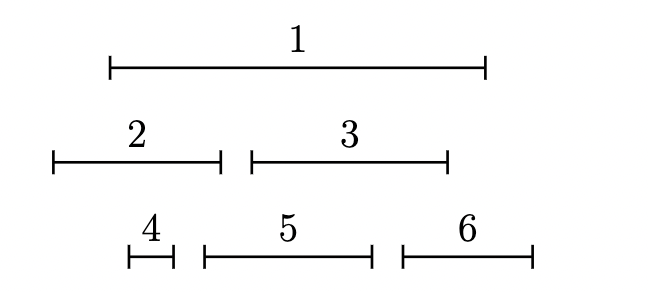
Convex hull¶
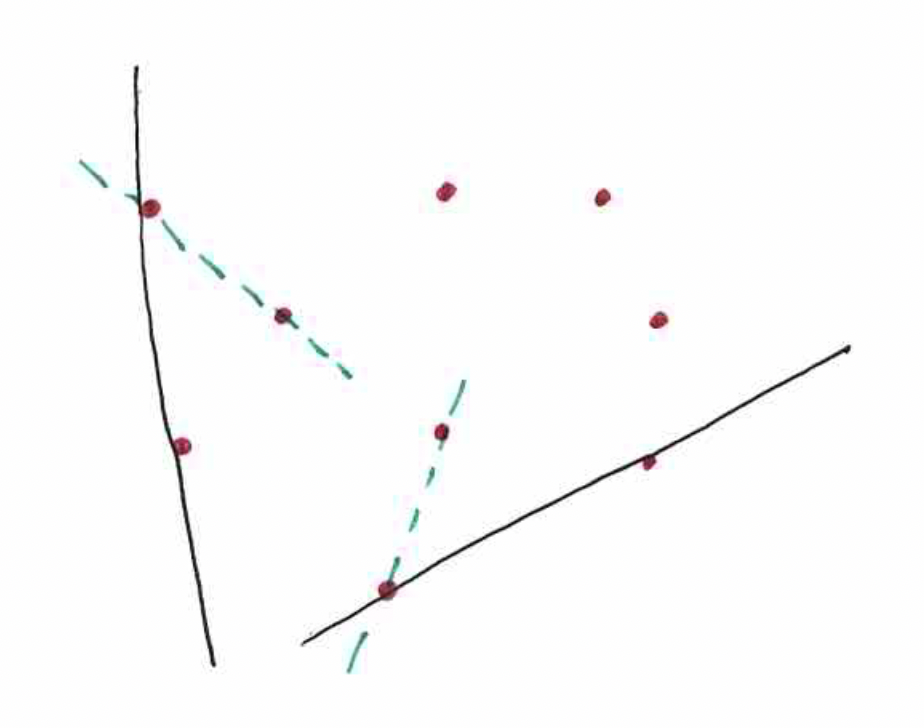
Median finding¶
Runtime: O($n^2$)
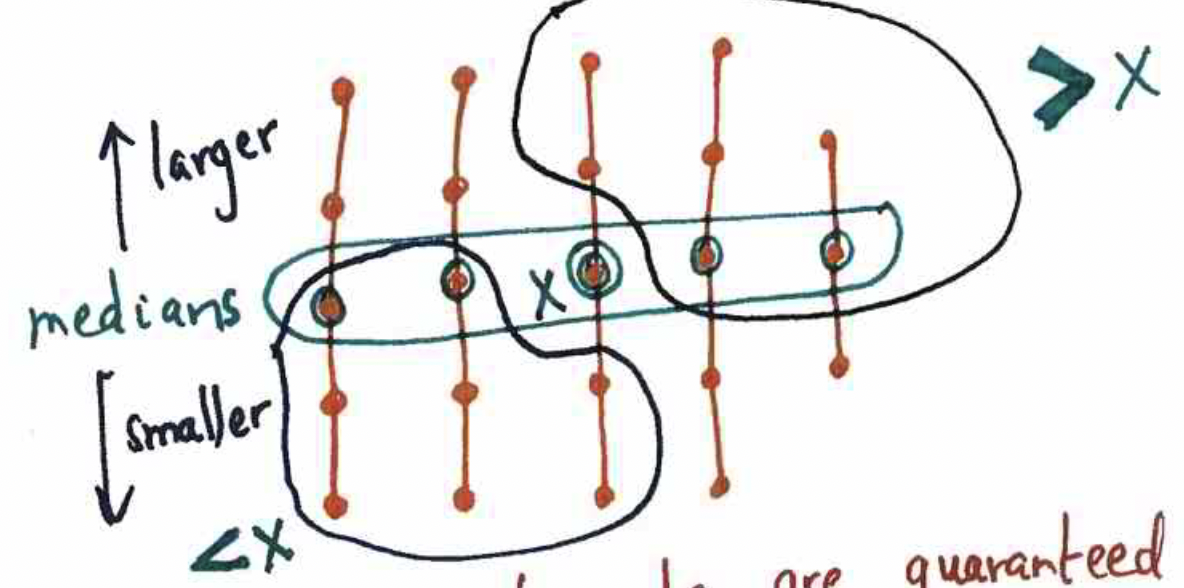
R1: methods¶
smarter IS¶
recursion tree: reduce the runtime to O(logn)
1 | M[j] = max(w(j) + M[p(j)], M[j - 1]) for j=1 to n |
Strassen’s algorithm¶
- multiplication runs much slower than addition
- Strassen’s only uses 7 multiplications instead of 8
Master theorem¶
- Old stuff of 6.006
Fast Fourier Transform¶
-
polynomial representations
- Coefficient vector
- Roots and a scale term: A(x) = ( x − $r_0$) · (x − $r_1$) · · · · · (x −$ r_{n−1}$) · c
- Samples: (x0, y0), (x1, y1), . . . , ( xn−1, yn−1) with A(xi) = yi (∀i) , xi is distinct.
-
Operations: evaluation; addition; multiplication
-
Conversion between coefficients and samples in O(nlgn) time

Polynomial multiplication¶
-
a divide and conquer algorithm: Divide into even and odd coefficients
-
Construct a collapsing set X
-
nth roots of unity: Euler’s formula
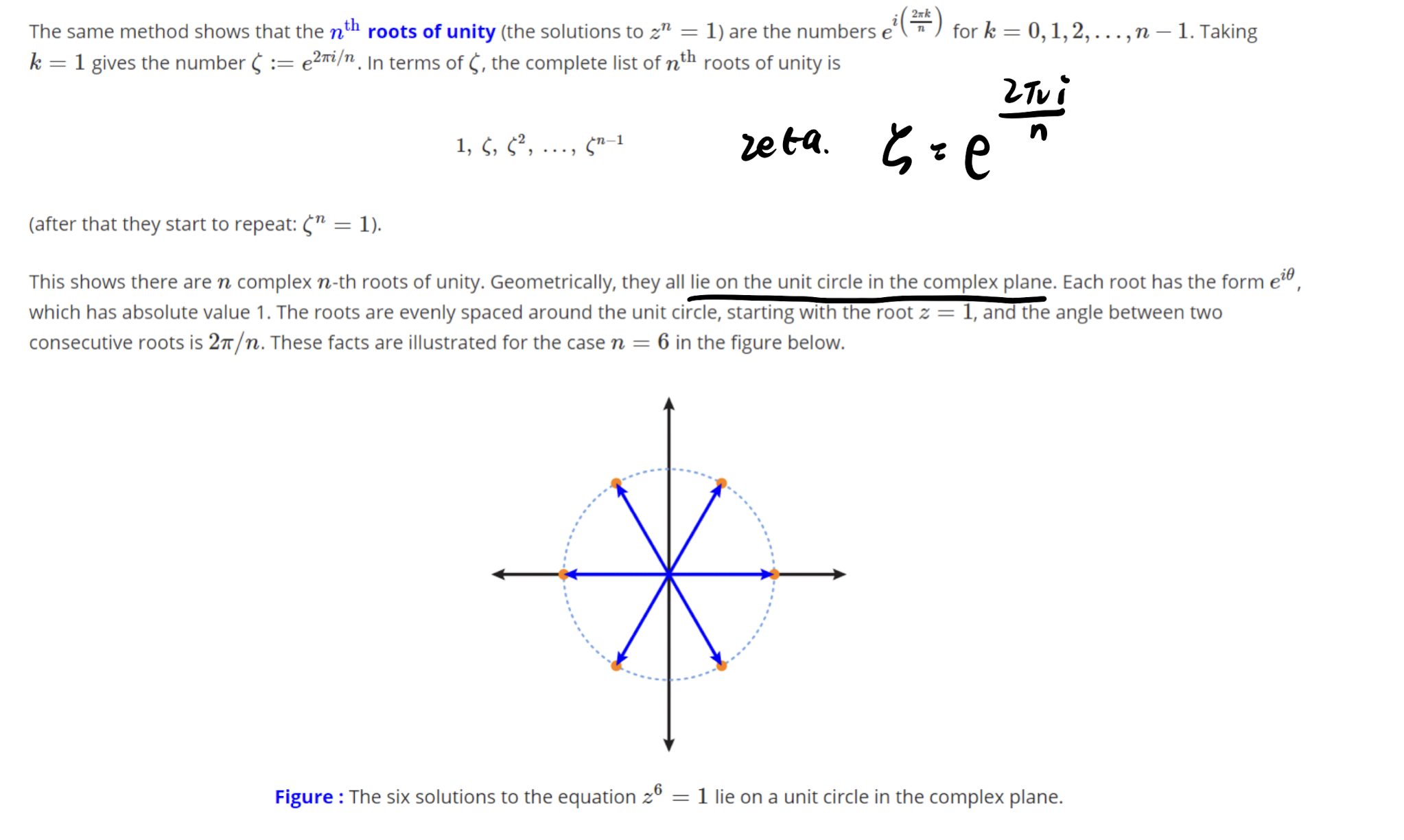
FFT¶
-
FFT: O(nlgn) divide and conquer algorithm for DFT
-
Discrete Fourier Transform: computing A → A* = V · A for $x_k = e^{iτk/n}$ where n = $2^l$, where A is the set of coefficients and
A* is the resulting samples. -
Inverse Discrete Fourier Transform: A* → $V^ {−1}$ · A* = A
$V^ {−1}$ = 1/n * complex conjugate of V
-
Fast Polynomial Multiplication
- A* = FFT(A), B* = FFT(B)
- c_k* = a_k* b_k * for k = 0, 1, …, n-1
- C = IFFT(c*)
application¶
- audio processing
Van Emade Boas Tree¶
problem: why use b tree instead of bst in practice?
答案与内存层级有关。通常的算法中我们假定从内存中直接获取数据,而实际上计算机的基本内存结构包括:cpu与缓存器间的高速通道,缓存与磁盘中的低速通道。每次访问磁盘获取数据的花费都很大,所以我们需要减少磁盘的访问,因而引入了缓存器。然后我们需要将需要的内存块从磁盘带到缓存中,当块的大小与cache line size相同时,能更大的利用访问的花费。
二叉树的存储方式是逐层存储的,一个分支对应一个数据。而b tree可以将整个块存储在同个分支,这样能更快的带出需要的内存块而不需要逐次访问磁盘。
Structure¶
-
B represents branching factor, which is related to cache line length. ex:in 2-3 tree: B = 2
- All leaves are at the same level
-
Operation: how to delete node?
-
move deletion to the leaves.
Successor: leftmost in the right subtree or rightmost in the left subtree.
-
Case1: have sibling tree undersell
-
Case2: don’t have sibing tree underfull -> merge: propagate the emptiness up, merge; if sibling tree is underfull, rotate.
-
Analysis¶
We want to maintain n elements in the range {0, 1, 2, . . . , u − 1} and perform Insert, Delete and Successor operations in O(log log u) time.
Intuition: binary search on the levels of tree.
Improvements: how a very simple data structure become vEB tree?
-
Bit vector: We maintain a vector V of size u such that V[x] = 1 if and only if x is in the set.
-
Split Universe into Clusters: splitting up the range {0, 1, 2, . . . , u − 1} into sqrt(u) clusters of size sqrt(u).
Then we have a summary vector.
1
2
3low(x) = x mod sqrt(u) = j
high(x) = x //(下取整)sqrt(u) = i
index(i,j) = i*sqrt(u) + jVersion 1:
Insert:
- Set V.cluster[ high(x) ] [ low(x) ] = 1
- Mark cluster high(x) as non-empty
Successor:
- Look within cluster high(x)
- Else, find next non-empty cluster i
- Find minimum entry j in that cluster
- Return index(i, j)
Version 2: use recursion: successor calls inside successor, insert calls inside insert.
V.cluster[i], V.summary, V.summary[i]
1
2
3
4
5
6
7
8
9
10
11INSERT(V, x)
1 Insert(V.cluster[high(x)], low[x])
2 Insert(V.summary, high[x])
SUCCESSOR(V, x)
1 i = high(x)
2 j = Successor(V.cluster[i], j)
3 if j = = ∞
4 i = Successor(V.summary, i)
5 j = Successor(V.cluster[i], −∞)
6 return index(i, j)then we have a problem: two recursive call in insert, three recursive call in successor. We want one recursive call to achieve our goal.
-
Maintain Min and Max: We store the minimum and maximum entry in each structure. This gives an O(1) time overhead for each Insert operation.
-
Don’t store Min recursively:
The Successor call now needs to check for the min separately.
if x < V.min : return V.min
space improvement: We can improve from Θ(u) to O(n log log u).
Intuition: for each element in n, perform a O(lglgu) runtime insertion.